Special CPM Seminar
Quantum limits of sensing and imaging
Animesh Datta
University of Warwick
Of the several quantum technological applications being pursued,
quantum-enhanced sensing and imaging is a prominent one. This is driven by its
much-anticipated applicability in fields such as sensor design, microscopy,
spectroscopy, and imaging, as well as the belief that the requirements for a
quantum-enhanced sensor are less demanding that those for a universal quantum
computer or simulator. The latter is based on numerous studies over the
years [1], but almost entirely concerned with the problem
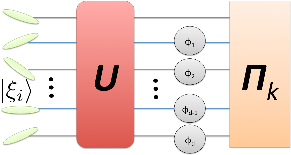
of estimating a single-phase parameter. Going beyond these, we present some
of our recent results on the quantum limits of estimating multiple parameters
simultaneously. Since most technological sensing applications involve multiple
parameters, this understanding is vital.
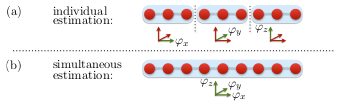
More quantum enhancement is attainable in the precision of estimating multiple
phases simultaneously as compared to a single phase. The additional enhancement
for simultaneous multiple phase estimation is proportional to the number of
phase parameters. More concretely, consider the problem of estimating d
phase parameters using quantum states across d + 1 modes. Let R
be the ratio of the variance of d phases simultaneously to that of
estimating them individually, subject to a total energy constraint. While
R ~ 1/d for general quantum states, for Gaussian states R
≤ 1/2. This is the first fundamental limitation for Gaussian states in
quantum estimation [2], similar to those known in quantum
computation and communication.
While for a single parameter it is always possible to devise a measurement
that attains the quantum-enhanced limit, for multiple parameters there is no
such guarantee. There are applications where the multiple phase parameters
of interest generated by operators that are mutually incompatible. Instances
include the 3 components of a rotation, magnetic fields, and accelerations.
This is a scenario that does not arise in single parameter sensing problems.
We show that it is indeed possible to design quantum probe states that can
estimate all non-commuting components of a multidimensional field simultaneously
at the quantum limit [3].
References:
[1] R. Demkowicz-Dobrzanski et al., Progress in
Optics 345-435 (2015).
[2] C. N. Gagatsos, D. Branford, A. Datta, Phys. Rev. A
94, 42342 (2016).
[3] T. Baumgratz, A. Datta, Phys. Rev. Lett. 116, 30801
(2016).
Tuesday, September 5th 2017, 10:30
Ernest Rutherford Physics Building, room 326
|